Geometric Primitives

The Java 2D™ API provides a useful set of standard shapes such as points, lines, rectangles, arcs, ellipses, and curves. The most important package to define common geometric primitives is the java.awt.geom package. Arbitrary shapes can be represented by combinations of straight geometric primitives.

The Shape interface represents a geometric shape, which has an outline and an interior. This interface provides a common set of methods for describing and inspecting two-dimensional geometric objects and supports curved line segments and multiple sub-shapes. The Graphics class supports only straight line segments. The Shape interface can support curves segments.

For more details about how to draw and fill shapes, see the Working with Geometry lesson.

Points

The Point2D class defines a point representing a location in (x, y) coordinate space. The term “point” in the Java 2D API is not the same as a pixel. A point has no area, does not contain a color, and cannot be rendered.

Points are used to create other shapes. ThePoint2D class also includes a method for calculating the distance between two points.

Lines

The Line2D class is an abstract class that represents a line. A line’s coordinates can be retrieved as double. The Line2D class includes several methods for setting a line’s endpoints.

Also, you can create a straight line segment by using the GeneralPath class described below.

Rectangular Shapes

The Rectangle2D, RoundRectangle2D, Arc2D, and Ellipse2D primitives are all derived from the RectangularShape class. This class defines methods for Shape objects that can be described by a rectangular bounding box. The geometry of a RectangularShape object can be extrapolated from a rectangle that completely encloses the outline of the Shape.

Quadratic and Cubic Curves

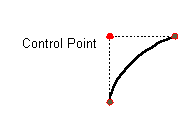
The QuadCurve2D enables you to create quadratic parametric curve segments. A quadratic curve is defined by two endpoints and one control point.

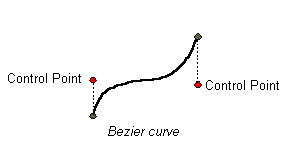
The CubicCurve2D class enables you to create cubic parametric curve segments. A cubic curve is defined by two endpoints and two control points. The following are examples of quadratic and cubic curves. See Stroking and Filling for implementations of cubic and quadratic curves.

This figure represents a quadratic curve.

This figure represents a cubic curve.

Arbitrary Shapes

The GeneralPath class enables you to construct an arbitrary shape by specifying a series of positions along the shape’s boundary. These positions can be connected by line segments, quadratic curves, or cubic (Bézier) curves. The following shape can be created with three line segments and a cubic curve. See Stroking and Filling for more information about the implementation of this shape.

Areas

With the Area class, you can perform boolean operations, such as union, intersection, and subtraction, on any two Shape objects. This technique, often referred to as constructive area geometry, enables you to quickly create complex Shape objects without having to describe each line segment or curve.