Creating a Client Program
Two separate classes make up the client in our example. The first
class, ComputePi, looks up and invokes a
Compute object. The second class, Pi,
implements the Task interface and defines the work to be
done by the compute engine. The job of the Pi class is to
compute the value of
to some number of decimal places.
The non-remote
Task
package compute;
public interface Task<T> {
T execute();
}
The code that invokes a Compute object's methods must obtain
a reference to that object, create a Task object, and then
request that the task be executed. The definition of the task class
Pi is shown later. A Pi object is constructed
with a single argument, the desired precision of the result. The result
of the task execution is a java.math.BigDecimal
representing
calculated to the specified precision.
Here is the source code for
client.ComputePi
package client;
import java.rmi.registry.LocateRegistry;
import java.rmi.registry.Registry;
import java.math.BigDecimal;
import compute.Compute;
public class ComputePi {
public static void main(String args[]) {
if (System.getSecurityManager() == null) {
System.setSecurityManager(new SecurityManager());
}
try {
String name = "Compute";
Registry registry = LocateRegistry.getRegistry(args[0]);
Compute comp = (Compute) registry.lookup(name);
Pi task = new Pi(Integer.parseInt(args[1]));
BigDecimal pi = comp.executeTask(task);
System.out.println(pi);
} catch (Exception e) {
System.err.println("ComputePi exception:");
e.printStackTrace();
}
}
}
Like the ComputeEngine server, the client begins by
installing a security manager. This step is necessary because the process
of receiving the server remote object's stub could require downloading
class definitions from the server. For RMI to download
classes, a security manager must be in force.
After installing a security manager, the client constructs a name to
use to look up a Compute remote object, using the same
name used by ComputeEngine to bind its remote object.
Also, the client uses the LocateRegistry.getRegistry API to
synthesize a remote reference to the registry on the server's
host. The value of the first command-line argument,
args[0], is the name of the remote host on which the
Compute object runs. The client then invokes the
lookup method on the registry to look up the remote
object by name in the server host's registry. The
particular overload of LocateRegistry.getRegistry used,
which has a single String parameter, returns a
reference to a registry at the named host and the default registry
port, 1099. You must use an overload that has an int
parameter if the registry is created on a port other than 1099.
Next, the client creates a new Pi object, passing to the
Pi constructor the value of the second command-line
argument, args[1], parsed as an integer. This argument
indicates the number of decimal places to
use in the calculation. Finally, the client invokes the
executeTask method of the Compute remote
object. The object passed into the executeTask invocation
returns an object of type BigDecimal, which the program
stores in the variable result. Finally, the program
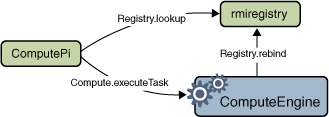
prints the result. The following figure depicts the flow of
messages among the ComputePi client, the
rmiregistry, and the ComputeEngine.
The Pi class implements the Task
interface and computes the value of
to a specified number of decimal places. For this example, the actual
algorithm is unimportant. What is important is that the algorithm is
computationally expensive, meaning that you would
want to have it executed on a capable server.
Here is the source code for
client.PiTask interface:
package client;
import compute.Task;
import java.io.Serializable;
import java.math.BigDecimal;
public class Pi implements Task<BigDecimal>, Serializable {
private static final long serialVersionUID = 227L;
/** constants used in pi computation */
private static final BigDecimal FOUR =
BigDecimal.valueOf(4);
/** rounding mode to use during pi computation */
private static final int roundingMode =
BigDecimal.ROUND_HALF_EVEN;
/** digits of precision after the decimal point */
private final int digits;
/**
* Construct a task to calculate pi to the specified
* precision.
*/
public Pi(int digits) {
this.digits = digits;
}
/**
* Calculate pi.
*/
public BigDecimal execute() {
return computePi(digits);
}
/**
* Compute the value of pi to the specified number of
* digits after the decimal point. The value is
* computed using Machin's formula:
*
* pi/4 = 4*arctan(1/5) - arctan(1/239)
*
* and a power series expansion of arctan(x) to
* sufficient precision.
*/
public static BigDecimal computePi(int digits) {
int scale = digits + 5;
BigDecimal arctan1_5 = arctan(5, scale);
BigDecimal arctan1_239 = arctan(239, scale);
BigDecimal pi = arctan1_5.multiply(FOUR).subtract(
arctan1_239).multiply(FOUR);
return pi.setScale(digits,
BigDecimal.ROUND_HALF_UP);
}
/**
* Compute the value, in radians, of the arctangent of
* the inverse of the supplied integer to the specified
* number of digits after the decimal point. The value
* is computed using the power series expansion for the
* arc tangent:
*
* arctan(x) = x - (x^3)/3 + (x^5)/5 - (x^7)/7 +
* (x^9)/9 ...
*/
public static BigDecimal arctan(int inverseX,
int scale)
{
BigDecimal result, numer, term;
BigDecimal invX = BigDecimal.valueOf(inverseX);
BigDecimal invX2 =
BigDecimal.valueOf(inverseX * inverseX);
numer = BigDecimal.ONE.divide(invX,
scale, roundingMode);
result = numer;
int i = 1;
do {
numer =
numer.divide(invX2, scale, roundingMode);
int denom = 2 * i + 1;
term =
numer.divide(BigDecimal.valueOf(denom),
scale, roundingMode);
if ((i % 2) != 0) {
result = result.subtract(term);
} else {
result = result.add(term);
}
i++;
} while (term.compareTo(BigDecimal.ZERO) != 0);
return result;
}
}
Note that all serializable classes, whether they implement the
Serializable interface directly or indirectly, must
declare a private static final
field named serialVersionUID to guarantee
serialization compatibility between versions. If no previous version
of the class has been released, then the value of this field can be
any long value, similar to the 227L used by
Pi, as long as the value is used consistently in
future versions. If a previous version of the class has been released
without an explicit serialVersionUID declaration, but
serialization compatibility with that version is important, then the
default implicitly computed value for the previous version must be
used for the value of the new version's explicit declaration. The
serialver tool can be run against the previous version to
determine the default computed value for it.
The most interesting feature of this example is that the
Compute implementation object never needs the Pi class's
definition until a Pi object is passed in as an argument
to the executeTask method. At that point, the code for the
class is loaded by RMI into the Compute object's Java virtual
machine, the execute method is invoked, and the task's code
is executed. The result, which in the case of
the Pi task is a BigDecimal object,
is handed back to the calling client, where it is used to print the
result of the computation.
The fact that the supplied Task object computes the value
of Pi is irrelevant to the ComputeEngine
object. You could also implement a task that, for example, generates a
random prime number by using a probabilistic algorithm. That task would also
be computationally intensive and therefore a good candidate for passing
to the ComputeEngine, but it would require very
different code. This code could also be downloaded when the
Task object is passed to a Compute object.
In just the way that the algorithm for computing
is brought in when needed, the code that generates the random prime
number would be brought in when needed. The Compute
object knows only that each object it receives implements the
execute method. The Compute object does not
know, and does not need to know, what the implementation does.
